T1 密码锁(lock)
题意
对于一个由 $0\sim9$ 组成的五位数密码(假设 $9$ 的下一位是 $0$,即密码位的运算在 $\text{mod }10$ 意义下进行),我们可以进行一次以下两种操作之一:
-
将某一位数字增加一个值
-
将相邻的两位同时增加同一个值
现在题目有一个未知的原始密码,给你 $n$ 个密码($1\le n\le8$),其中每一个都是由原始密码经过一次上述操作之一后产生的,问你原始密码有多少种可能。
做法一
思路
由于密码只有五位数,我们当然可以枚举所有的五位数密码,然后再判断给的 $n$ 个密码是否都可以通过当前枚举到的密码经过一次操作后产生。
这样的复杂度是 $O(10^5n)$ 的,时间上毫无压力,写起来也很简单,逻辑理清即可,期望得分 $100\text{pts}$。
需要注意的是,题目给出的 $n$ 个密码本身并不是正确答案。
代码
#include<cstdio>
using namespace std;
int n, s[10][10], ans;
inline bool check(int a, int b, int c, int d, int e) {
for(int i=1; i<=n; ++i) {
int delta = (a!=s[i][1])+(b!=s[i][2])+(c!=s[i][3])+(d!=s[i][4])+(e!=s[i][5]);
if(delta<1 || delta>2) return false;
if(delta == 2) {
int ad=(a-s[i][1]+10)%10, bd=(b-s[i][2]+10)%10, cd=(c-s[i][3]+10)%10, dd=(d-s[i][4]+10)%10, ed=(e-s[i][5]+10)%10;
if(!((ad&&ad==bd) || (bd&&bd==cd) || (cd&&cd==dd) || (dd&&dd==ed))) return false;
}
}
return true;
}
int main() {
scanf("%d", &n);
for(int i=1; i<=n; ++i)
for(int j=1; j<=5; ++j) scanf("%d", &s[i][j]);
for(int a=0; a<=9; ++a)
for(int b=0; b<=9; ++b)
for(int c=0; c<=9; ++c)
for(int d=0; d<=9; ++d)
for(int e=0; e<=9; ++e) {
if(check(a, b, c, d, e)) ++ans;
}
printf("%d", ans);
return 0;
}
做法二
思路
注意到,如果一个密码串 A 经过一次操作后可以变成密码串 B,那么显然密码串 B 也可以通过一次该操作的逆操作后变成密码串 A。
分析样例一,我们发现,一个密码串经过一次操作后有 $81$ 种可能。
结合这两点,我们得到一个启示,可以对于给出的 $n$ 个密码中的每一个,枚举其经过一次操作后所有可能得到的密码串(我们知道这有 $81$ 种)。如果某个密码串被所有 $n$ 个密码都枚举到过,反过来即代表这 $n$ 个密码都可以由该密码串经过一次操作后得到,那么这个密码串就是原始密码的一种可能。
具体实现,我们可以使用一个计数器来保存某个密码串被枚举到的次数,当次数增加到 $n$ 时,$ans \gets ans+1$,这样的复杂度是 $O(81n)$ 的,比做法一快了一千倍(尽管两种做法都是线性的),实现起来也要简单得多,期望得分 $100\text{pts}$。
代码
#include<cstdio>
using namespace std;
int n, cnt[10][10][10][10][10], ans;
inline void add(int a, int b, int c, int d, int e) {
if(++cnt[a%10][b%10][c%10][d%10][e%10] == n) ++ans;
}
int main() {
scanf("%d", &n);
for(int i=1, a, b, c, d, e; i<=n; ++i) {
scanf("%d%d%d%d%d", &a, &b, &c, &d, &e);
for(int j=1; j<10; ++j) {
add(a+j, b, c, d, e);
add(a, b+j, c, d, e);
add(a, b, c+j, d, e);
add(a, b, c, d+j, e);
add(a, b, c, d, e+j);
add(a+j, b+j, c, d, e);
add(a, b+j, c+j, d, e);
add(a, b, c+j, d+j, e);
add(a, b, c, d+j, e+j);
}
}
printf("%d", ans);
return 0;
}
T2 消消乐(game)
题意
我们称一个字符串是可消除的,当且仅当可以对这个字符串进行若干次操作,使之成为一个空字符串。
其中每次操作可以从字符串中删除两个相邻的相同字符,操作后剩余字符串会拼接在一起。
现在,给你一个长度为 $n$ 的仅由小写字母构成的字符串($1\le n\le2\times10^6$),求其可消除的非空连续子串的个数。
做法一
思路
据说该题存在两道很像的题目,如果你做过其中一题,亦或是你自己发现了"对于一个字符,与其左/右第一个未被匹配的相同字符匹配一定更优“这个结论,那么我们就可以得知”可消除字符串“的另一种定义:
创建一个空栈,按顺序枚举字符,若与栈顶字符相同则弹出栈顶字符,否则将其入栈,若最后栈为空,则这个字符串是可消除的。
如何证明上述结论呢,其实很简单。假设字符串中存在三个相同的的未匹配字符 $i,j,k$($i \lt j \lt k$),那么显然此时 $j$ 应该和 $i$ 或 $k$ 配对,否则若 $i$ 和 $k$ 配对的话,由于中间夹着个 $j$ 未配对,$i$ 和 $k$ 是无法相邻并清除掉的。
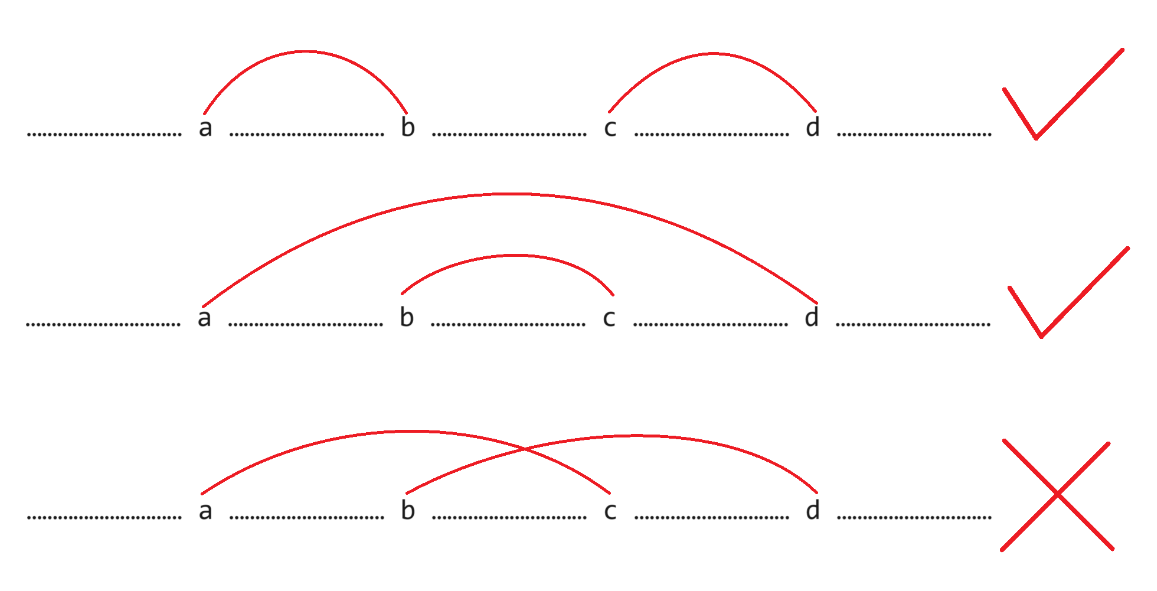
至于存在四个的情况,可以用一张图片解释:
对于四个相同的字符 $a,b,c,d$($a\lt b\lt c\lt d$),显然只能按图中第一第二种情况配对,若按第三种情况配对会导致无法消除。
当 $a,b$ 之间的字符串 $[a+1,b-1]$ 以及 $c,d$ 之间的字符串 $[c+1,d-1]$ 可消除时,$a$ 和 $b$ 会匹配,之后 $c$ 和 $d$ 会匹配,此时为上图中第一种情况。
当 $b,c$ 之间的字符串 $[b+1,c-1]$ 可消除时,$b$ 和 $c$ 会匹配,若再进一步 $[a+1,b-1]\cup [c+1,d-1]$ 也可消除时,此时 $[a+1,d-1]$ 整个串可消除,$a$ 和 $d$ 便可匹配,此时为上图中第二种情况。
当然这里证明的并不严谨,我们可以感性去理解。
在这个结论下,我们得到可消除串的另一定义。我们按照该定义去模拟,可以实现一种枚举起点,往右拓展,通过判断当前栈是否为空来得到当前区间是否可消除的做法,时间复杂度为 $O(n^2)$,期望得分 $50\text{pts}$。
代码
#include<cstdio>
#include<stack>
using namespace std;
int n;
long long ans;
char s[2000005];
int main() {
scanf("%d%s", &n, s+1);
for(int i=1; i<n; ++i) {
stack<int> stk;
for(int j=i; j<=n; ++j) {
if(stk.size() && stk.top()==s[j]-'a') stk.pop();
else stk.push(s[j]-'a');
if(stk.empty()) ++ans;
}
}
printf("%lld", ans);
return 0;
}
做法二
思路
在模拟做法一的栈时,我们发现枚举时如果经过一段可消除的字符串,栈会不断地加入一段字符后弹出一段字符,或者先弹出一段字符后加回来一段字符。总之,最终枚举完这一段可消除串之后,所有在这段时间内入栈的字符都被出栈了,或是所有被出栈的字符最后又都加回来了。
这启示我们,初始的栈不一定需要是一个空栈,只要经过一段区间前后的栈相同,那么这段区间就是可被消除的。
那么如何判断两个栈是否相同呢?对于一个存放字符类型的栈,其实就类似于一个字符串类型,可以在末尾插入或删除字符。因此我们可以对栈进行类似于字符串哈希的做法,同时记录所有哈希值出现的次数,那么答案就很好统计了。
我们在枚举字符的时候,可以同时进行按照出入栈的方式计算当前栈的哈希值,因此这样的做法是线性的,时间复杂度为 $O(n)$,期望得分 $100\text{pts}$。
这里需要注意的是,自然溢出单哈希极其容易被卡(阅读他人游记时听说存在一种串可以卡掉任意 $base$ 的自然溢出哈希),例如本次比赛只使用 $998244353$ 自然溢出哈希会被官方数据卡至 $85pts$,而洛谷自测中会被卡至 $55\text{pts}$,因此建议在任何自然溢出哈希中使用双哈希甚至三哈希。
对于出题,卡单哈希很没素质,而如果连双哈希都卡就属于不讲武德了。下面的代码使用了双哈希,洛谷自测得分 $100\text{pts}$。
代码
#include<cstdio>
#include<stack>
#include<map>
#define N 2000005
using namespace std;
typedef unsigned long long ull;
const ull key1=998244353, key2=1e9+7;
int n, top;
ull h1[N], h2[N], now1, now2, ans;
char s[N];
stack<int> stk;
map<ull, ull> cnt;
int main() {
scanf("%d%s", &n, s+1);
h1[1]=h2[1]=1, cnt[0]=1;
for(int i=2; i<=n; ++i) h1[i]=h1[i-1]*key1, h2[i]=h2[i-1]*key2;
for(int i=1; i<=n; ++i) {
int x = s[i]-'a'+1;
if(stk.size() && stk.top()==x) now1-=h1[top]*x, now2-=h2[top--]*x, stk.pop();
else now1+=h1[++top]*x, now2+=h2[top]*x, stk.push(x);
ans+=cnt[now1*now2], ++cnt[now1*now2];
}
printf("%llu", ans);
return 0;
}
做法三
思路
延续上一个做法的思路,但我们将观点移动到字典树上。
我们比较一个字符串的方式,除了字符串哈希外,也可以使用字典树。若两个字符串同时从根节点开始在字典树上匹配,最终处于同一个节点,即这两个字符串对应在字典树中的状态是相同的,那么这两个字符串便是相同的。
对于入栈和出栈操作,在字典树上就对应了向下走到子节点和向上走回父节点;而栈中的栈顶,就对应了字典树中当前节点的入边(即连向父节点的边)的边权。
这样,我们枚举字符串时的出栈入栈其实相当于在字典树上进行移动!只需要记录某一个节点经过的次数,即可统计答案。
该做法时间复杂度为 $O(n)$,空间复杂度为 $O(n|\Sigma|)$,期望得分 $100\text{pts}$。
代码
#include<cstdio>
#define N 2000005
using namespace std;
int n, t[N][26], fa[N], fc[N], tot;
long long ans, cnt[N];
char s[N];
int main() {
scanf("%d%s", &n, s+1);
cnt[0] = 1;
for(int i=1, u=0; i<=n; ++i) {
int x = s[i]-'a';
if(u && x==fc[u]) u = fa[u];
else {
int &p = t[u][x];
if(!p) p=++tot, fa[p]=u, fc[p]=x;
u = p;
}
ans+=cnt[u], ++cnt[u];
}
printf("%lld", ans);
return 0;
}
做法四
思路
做法四与前三个做法并不相同,但有用到做法一中的结论。接下来文中的“可消除字符串“均指满足题目要求的非空连续子串。
我们考虑为“可消除”的字符串重新进行定义。令 $A,B$ 为可消除的字符串,$x$ 表示某个小写字母:
-
$xx$ 是可消除的
-
$xAx$ 是可消除的
-
$AB$ 是可消除的
这样的定义方式很清晰,但也容易出错。许多游记之中都有记载,包括我在内的许多人都得出过诸如“可消除的字符串一定是由多个偶回文串拼接而成”之类的错误结论。
假设 $A_i$ 为以字符串中以第 $i$ 个位置为结尾的最小的可消除字符串,并且设 $to_i$ 为 $A_i$ 的左端点,我们考虑如何统计包含 $A_i$ 的所有可消除串的数量。
根据定义,除了 $A_i$ 以外,所有以 $to_i-1$ 这个位置为结尾的可消除串,都可以通过拼上 $A_i$,即定义中的 $AB$ 这种形式来合成一个更大的可消除串,因此我们当然可以设 $f_i$ 表示以 $i$ 这个位置结尾的可消除字符串的数量,这样就可以通过 $f_i\gets f_{to_i-1}+1$ 转移答案,同时也表示出了 $i$ 这个位置对答案的贡献。
那么这个 $to_i$ 要怎么求呢?我们考虑已经求出了前 $i-1$ 个位置,现在求第 $i$ 个位置。显然,$A_i$ 要么是 $xx$ 的形式要么是 $xAx$ 的形式。
根据我们做法一的结论,我们应该优先匹配最近的。若 $i-1$ 与 $i$ 相同则匹配,此时为 $xx$ 形式;否则我们应该考虑所有以 $i-1$ 位置为结尾的可消除字符串,尝试按照 $xAx$ 的形式去匹配。
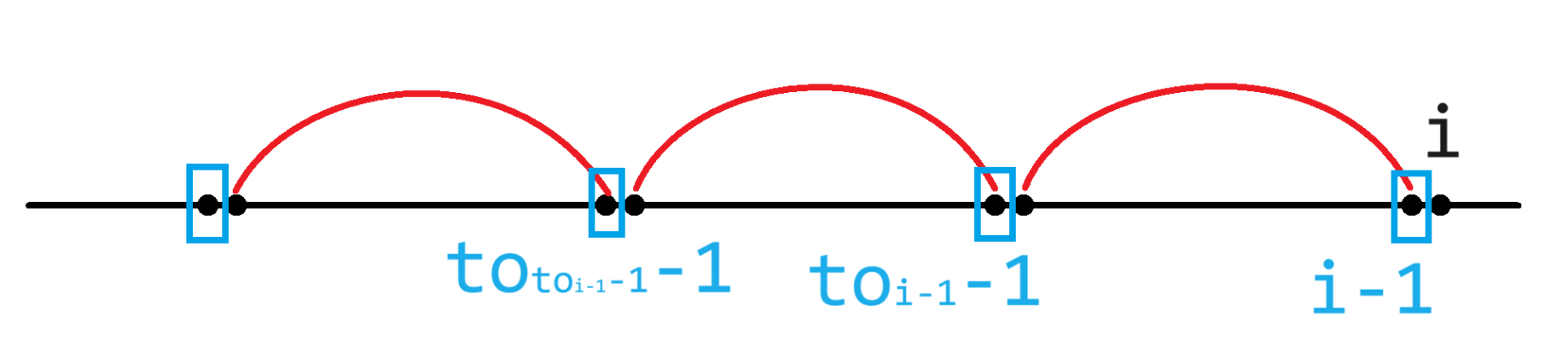
因此,我们只需要依次枚举 $i-1,to_{i-1}-1,to_{to_{i-1}-1}-1\cdots$ 的字符,判断其是否相同即可,具体而言,枚举的位置如下图:
上图中红色弧表示一段最短可消除子串,蓝色方框表示可以尝试匹配的位置。由图可以直观看出来,若在这些蓝色方框之中存在一个最大的位置 $j$,满足 $j$ 与 $i$ 的字符相同,那么显然 $A_i$ 就是 $[j,i]$ 了,就可以通过 $to_i\gets j$ 来维护左端点,同时按先前所说 $f_i\gets f_{j-1}+1$ 来转移答案了。
综上,我们在枚举到 $i$ 的时候,一直往前跳找到第一个可以匹配的,就可以维护 $to_i$ 和 $f_i$,对 $f_i$ 进行求和便是最终答案。
由于我们需要向前跳,因此时间复杂度看起来像 $O(n^2)$,但实际上我们往前跳的次数是有限的,所以实际应该是线性或者近似线性的?我不会证,但是能过。
当然,这是可以优化的,我们可以把跳跃的过程做个压缩:由于 $i$ 位置上的字符只有 $26$ 种可能,因此对于 $i-1$ 这个位置开始的跳跃,我们最多有 $26$ 个目标位置,我们将这 $26$ 个目标位置称为 $i-1$ 这个位置的匹配序列,我们将 $to_{i,c}$ 更改为表示 $i$ 的匹配序列中,字符 $c$ 对应的目标位置。
注意到对于 $i-1$ 这个位置,后续的跳跃是固定的,也就是 $i-1$ 的匹配序列是固定的,我们可以考虑维护这个东西。
设 $i$ 往左的第一个跳跃点是 $j$,字符串第 $i$ 个字符为 $s_i$。
我们发现,在先前跳跃的过程中,只要 $i$ 不能被匹配,即要匹配的字符不是 $s_i$,我们总会跳到 $j$,而接下来的跳跃和匹配过程实际上是相同的。
而其中的 $j$,实际上就是以 $i$ 结尾的最短可消除字符串的左端点,也就是 $to_{i-1,s_i}$。
因此,这个东西就可以转移了:
$$ to_{i,x}=\begin{cases} i & x=s_i \\ to_{j,x} & x\neq s_i \end{cases} $$
其中 $j=to_{i-1,s_i}$。实际上,我们就是在做类似于倍增一样的优化。
具体实现起来并不难,枚举到 $i$,令 $j\gets to_{i-1,s_i}$,那么我们就可以通过 $j$ 转移出 $f_i$ 和 $to_{i,x}$,此时以 $i$ 为结尾的可消除字符串的贡献就是 $f_i$,求和即可。时空复杂度 $O(n|\Sigma|)$,期望得分 $100\text{pts}$。
当然,实现时我们要注意可能并不存在以 $i$ 结尾的可消除字符串,判断一下即可。
代码
#include<cstdio>
#define N 2000005
using namespace std;
int n, to[N][26], c;
char s[N];
long long f[N], ans;
int main() {
scanf("%d%s", &n, s+1);
for(int i=1; i<=n; ++i) {
c=s[i]-'a', to[i][c]=i;
int p = to[i-1][c];
if(p) {
f[i] = f[p-1]+1;
for(int j=0; j<26; ++j)
if(j != c) to[i][j] = to[p-1][j];
}
ans += f[i];
}
printf("%lld", ans);
return 0;
}
T3
题意
太长就不放出来了,而且形式化题意写的挺好的。
思路
注意到 $n\le100$,那么这题就按照题意模拟即可。注意到 $addr\le10^{18}$,这题甚至有可能会爆 long long,考虑使用 unsigned long long 甚至 __int128。
这题实现难度并不高(实现上只有 STL 使用和操作三的字符串分割可能会有难度),主要难在思维逻辑上。对于这一类大模拟题目,我们想清楚如何实现,踏踏实实一步步做即可。
首先考虑如何维护一个结构体类型,不难总结出,一个结构体的所有信息为:
-
结构体类型的名字,并且我们只需要从名字找到结构体,而不用反过来得知结构体的名字
-
结构体类型的内存大小和对齐要求
-
结构体类型的所有成员,需要从名字能找到对应成员,还需要得知每一个成员在结构体中占内存的范围
我们考虑使用 struct 来维护这些信息,考虑到我们需要在结构体中套结构体,因此我们使用其在数组中的下标来作为其编号。
由于我们不需要得知结构体的名字,只需要由名字找到结构体,因此这里可以考虑使用 map<string, int> 来建立名字到结构体编号的映射关系。
对于成员变量,由于其大小和对齐要求已知,实际上我们只要保持其按照定义时的顺序,那么每一个成员变量在结构体中的地址其实是可以通过模拟来找到的,因此这里可以考虑使用 vector<pair<string, int> > 来存储其成员。
struct Type {
ull siz, st;
vector<pair<string, int> > mem;
} ty[110];
map<string, int> types;
同时我们注意到,初始的四种类型也同样需要维护大小和对齐要求,我们可以将其当做没有成员类型的结构体,这样就可以很方便的进行嵌套了!
int tcnt;
inline int newType(string name, ull siz, ull st) {
++tcnt;
ty[tcnt].siz=siz, ty[tcnt].st=st, types[name]=tcnt;
return tcnt;
}
int main() {
newType("byte", 1, 1);
newType("short", 2, 2);
newType("int", 4, 4);
newType("long", 8, 8);
...
}
这样,对于操作四,我们也可以方便的通过判断其编号是否 $\le 4$ 来判断是否为基础类型。
再来考虑维护一个变量,我们需要得知其起始名称地址及类型,同样的方式进行维护:
ull memory; //表示当前空间起始地址
struct Variable {
string name;
int type;
ull st;
} var[110];
map<string, int> vars;
int vcnt;
inline int newVar(string name, int t) {
++vcnt;
if(memory%ty[t].st) memory += ty[t].st-memory%ty[t].st; //放入前先对齐
var[vcnt].name=name, var[vcnt].type=t, var[vcnt].st=memory, vars[name]=vcnt;
memory += ty[t].siz;
return vcnt;
}
并且此时,var 数组内本身就是按照定义的顺序来排序的,这也方便了我们操作四对地址进行查找。
那么接下来,对于四个操作,我们一一进行分析:
-
按照题目要求定义一个新的类型即可,其对齐要求为所有成员中的最大值,其大小在添加成员时累加即可,注意这里各种地方都要对齐。
-
按照题目要求定义一个新的变量即可,这里我们维护了
var[i].st直接输出即可。 -
首先我们分割字符串,对于第一项,在
vars中找到该变量的类型和起始地址,从起始地址开始一层层往下递归,顺序枚举当前类型的成员,若为目标成员名字则进入,否则累加地址,注意这里各种地方都要对齐。 -
由于我们存储变量和类型成员时都是有序的,因此按照顺序向下递归找那个地址即可,注意这里各种地方都要对齐。
注意到各种地方都要对齐,因此建议写个对齐方法来节省代码。另外很多人喜欢用除法公式向下取整来对齐,我的建议是直接取模然后补到倍数就好了。
这一题实现起来说难不难,说简单不简单。其实这题的做法要多得多,我的也不是最简洁的,所以只是随便讲讲我考场上的实现思路。
因为懒得重写了,下面直接贴我的 $100\text{pts}$ 的考场代码,可能有些地方写的不好看。
代码
#include<iostream>
#include<map>
#include<vector>
using namespace std;
typedef unsigned long long ull;
struct Type {
ull siz, realsiz, st;
vector<pair<string, int> > mem;
} ty[110];
struct Variable {
string name;
int type;
ull st;
} var[110];
map<string, int> types, vars;
int n, opt, tcnt, vcnt;
ull memory;
inline int newType(string name, ull siz, ull st) {
++tcnt;
ty[tcnt].siz=siz, ty[tcnt].st=st, types[name]=tcnt;
return tcnt;
}
inline int newVar(string name, int t) {
++vcnt;
if(memory%ty[t].st) memory += ty[t].st-memory%ty[t].st;
var[vcnt].name=name, var[vcnt].type=t, var[vcnt].st=memory, vars[name]=vcnt;
memory += ty[t].siz;
return vcnt;
}
int main() {
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
newType("byte", 1, 1), newType("short", 2, 2), newType("int", 4, 4), newType("long", 8, 8);
for(cin>>n; n--;) {
cin >> opt;
if(opt == 1) {
string name, t;
int k;
ull siz=0, st=0;
cin >> name >> k;
int x = newType(name, 0, 0);
while(k--) {
cin >> t >> name;
int v = types[t];
if(siz%ty[v].st) siz += ty[v].st-siz%ty[v].st;
siz+=ty[v].siz, st=max(st, ty[v].st);
ty[x].mem.emplace_back(name, v);
}
ty[x].realsiz = siz;
if(siz%st) siz += st-siz%st;
ty[x].siz=siz, ty[x].st=st;
cout << siz << ' ' << st << '\n';
} else if(opt == 2) {
string t, name;
cin >> t >> name;
cout << var[newVar(name, types[t])].st << '\n';
} else if(opt == 3) {
string path, name;
ull st;
cin >> path;
int flag=0, x;
auto p = path.find(".");
while(p != string::npos) {
name=path.substr(0, p), path=path.substr(p+1);
if(!flag) x=vars[name], st=var[x].st, x=var[x].type;
else {
int v;
for(auto vt : ty[x].mem)
if(vt.first == name) {
v = vt.second;
break;
} else {
if(st%ty[vt.second].st) st += ty[vt.second].st-st%ty[vt.second].st;
st += ty[vt.second].siz;
}
if(st%ty[v].st) st += ty[v].st-st%ty[v].st;
x = v;
}
flag=1, p=path.find(".");
}
if(!flag) cout << var[vars[path]].st << '\n';
else {
int v;
for(auto vt : ty[x].mem)
if(vt.first == path) {
v = vt.second;
break;
} else {
if(st%ty[vt.second].st) st += ty[vt.second].st-st%ty[vt.second].st;
st += ty[vt.second].siz;
}
if(st%ty[v].st) st += ty[v].st-st%ty[v].st;
cout << st << '\n';
}
} else if(opt == 4) {
ull addr, st=0;
string ans;
cin >> addr;
if(addr >= memory) {
cout << "ERR" << '\n';
continue;
}
int x;
for(x=1; x<vcnt; ++x)
if(var[x].st<=addr && var[x+1].st>addr) break;
st+=var[x].st, ans+=var[x].name, x=var[x].type;
if(addr > st+ty[x].siz-1) {
cout << "ERR" << '\n';
continue;
}
int flag = 0;
while(x > 4) {
if(addr > st+ty[x].realsiz-1) {
cout << "ERR" << '\n';
flag = 1;
break;
}
int v;
for(auto vt : ty[x].mem) {
if(st%ty[vt.second].st) st += ty[vt.second].st-st%ty[vt.second].st;
if(addr < st) {
cout << "ERR" << '\n';
flag = 1;
break;
}
if(addr <= st+ty[vt.second].siz-1) {
v=vt.second, ans+="."+vt.first;
break;
} else {
st += ty[vt.second].siz;
}
}
x = v;
if(flag) break;
}
if(!flag) {
cout << ans << '\n';
}
}
}
return 0;
}
T4
题意
题目描述的很清楚,这里也不复述。
思路
首先我们注意到答案具有单调性:假设最少需要 $x$ 天完成任务,那么当我们使用的天数多于 $x$ 天时,任务是必然能够完成的,当我们使用的天数少于 $x$ 天时,任务是必然完不成的。
题目种保证答案 $\le10^9$,因此我们可以考虑二分答案,接下来就转换为指定一个完成任务的时间,能否高效地去判断能否完成任务。
我们观察这个式子:
$$ max(b_i+x\times c_i,1) $$
我们注意到,实际上 $b_i+x\times c_i$ 是一个一次函数,因此我们可以解不等式 $b_i+x\times c_i < 1$,得到当 $c_i\ne0$ 时,$x<\frac{1-b_i}{c_i}$。
我们对 $c_i$ 的正负进行分类讨论,可以得到上式取 $1$ 的范围,就可以对其进行求和,从而得到一段时间内生长的值:
$c_i=0$ 时,$\sum_{x=l}^r\max(b_i+c_ix,1)=b_i(r-l+1)$。否则,我们令 $p=\left\lfloor\frac{1-b_i}{c_i}\right\rfloor$,则有:
$$ \sum_{x=l}^r\max(b_i+c_ix,1)=\begin{cases} b_i(r-l+1)+\frac {c_i(l+r)(r-l+1)} 2 & c_i\gt0 \\ b_i(r-l+1)+\frac {c_i(l+r)(r-l+1)} 2 & c_i\lt0,r\lt p \\ b_i(p-l+1)+\frac {c_i(l+p)(p-l+1)} 2+r-p & c_i\lt0,l\le p\le r \\ r-l+1 & c_i\lt0,p\lt l\end{cases} $$
这个式子看起来有些复杂,但其实在纸上推的话很好推。
推出上述式子,我们就可以得知一段时间 $[l,r]$ 生长了多少了。因为我们已经指定了一个完成任务的时间,这个式子可以帮助我们通过解二次方程来得到一个节点最晚被种下的时间。
当然,谁解二次方程?你解吗?所以我们选择将上式用于 $O(1)$ 判断一棵树能否在给定时间段完成生成任务,再次对每个节点的最晚种植时间进行二分,得到每一个节点最晚被种下的时间。
注意到,我们会在前 $n$ 天每天种一棵树,因此某个叶子节点最晚一定会在第 $n$ 天被种植,因此最晚种植时间若 $\ge n$,实际上就等于毫无影响,我们将其取到 $n$,这样内层只需要在 $[1,n]$ 的范围内二分就行了。
当然,这里有个优化,我们可以在二分前先判断一次每一个节点第一天就种,最后能否达到目标,若这样都无法达到目标,那么这个指定的完成时间内是不可能完成任务的,直接返回 false 即可。
否则,我们就已经求出了所有节点最晚被种下的时间,此时就变成了树上的航空管制。
接下来其实就是要求一个种植顺序,满足所有节点都及时种下,并且父节点比子节点先被种下。
与航空管制的做法相同,我们贪心地将最晚被种下的时间最早,即最要紧的节点先种下。若最要紧的节点的父节点和祖先节点还未被种,就递归上去先把祖先节点和父节点种下即可。若种的过程中,存在某棵树没有及时种下,那么该任务就无法完成。
简单地证明一下这个贪心:由于我们任务要求所有树都及时种下,因为不管怎么样那些树都迟早得种,所以对于两棵树,先种其中更要紧的那一棵一定更优。
由于每一棵树只会被种一次,因此种树部分复杂度为 $O(n)$,而排序贪心部分复杂度为 $O(n\log n)$。
注意到最晚被种下的时间的值域被我们限制在了 $[1,n]$。因此我们可以将排序改为桶排序,消掉一个 $\log$,算上二分每个点最晚种植时间,内层的时间复杂度为 $O(n\log n+n)$。
因而总时间复杂度为 $O((n\log n+n)\log 10^9)$,期望得分 $100\text{pts}$。
代码
#include<cstdio>
#include<vector>
#include<algorithm>
#define N 100005
#define int long long
#define lll __int128
using namespace std;
inline int read() {
int x=0, f=1;
char ch = getchar();
while(ch<'0' || ch>'9') {
if(ch == '-') f = -1;
ch = getchar();
}
while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+(ch^48), ch=getchar();
return x*f;
}
struct Edge {
int v, nex;
} e[N<<1];
int n, vis[N], fa[N], b[N], c[N], idx, h[N], lst[N], cnt;
lll a[N];
inline void link(int u, int v) {
e[++idx]={v, h[u]}, h[u]=idx;
e[++idx]={u, h[v]}, h[v]=idx;
}
inline lll calc(int i, int l, int r) {
if(c[i] == 0) return (lll)b[i]*(r-l+1);
lll p = (1-b[i])/c[i];
if(c[i]>0 || r<p) return (lll)b[i]*(r-l+1)+(lll)c[i]*(l+r)*(r-l+1)/2;
else if(l > p) return r-l+1;
else return (lll)b[i]*(p-l+1)+(lll)c[i]*(l+p)*(p-l+1)/2+r-p;
}
void dfs(int u) {
for(int i=h[u]; i; i=e[i].nex) {
if(e[i].v == fa[u]) continue;
fa[e[i].v] = u;
dfs(e[i].v);
}
}
bool access(int u) {
if(!vis[fa[u]]) if(!access(fa[u])) return false;
if(++cnt > lst[u]) return false;
vis[u] = 1;
return true;
}
vector<signed> bk[N];
bool check(int limit) {
for(int i=1; i<=n; ++i) bk[i].clear();
cnt = 0;
for(int u=1; u<=n; ++u) {
if(calc(u, 1, limit) < a[u]) return false;
vis[u]=0, lst[u]=-1;
int l=1, r=n, mid;
while(l <= r) {
mid = (l+r)>>1;
if(calc(u, mid, limit) >= a[u]) lst[u]=mid, l=mid+1;
else r = mid-1;
}
bk[lst[u]].push_back(u);
}
for(int i=1; i<=n; ++i)
for(auto x : bk[i])
if(!vis[x] && !access(x)) return false;
return true;
}
signed main() {
n=read(), vis[0]=1;
for(int i=1; i<=n; ++i) a[i]=read(), b[i]=read(), c[i]=read();
for(int i=1; i<n; ++i) link(read(), read());
dfs(1);
int l=1, r=1e9, mid, ans;
while(l <= r) {
mid = (l+r)>>1;
if(check(mid)) ans=mid, r=mid-1;
else l = mid+1;
}
printf("%lld", ans);
return 0;
}
总结
本次题目考察的算法都不难,主要难在思维上,比较考验选手的做题量。
T1,感觉像是把普及组题放错了……大胆猜测是因为 $n$ 大了之后答案几乎全为 $1$ 或 $0$,为了避免去年不可以总司令的情况而将 $n$ 减小到 $\le8$。
T2,不管是三种正解还是 $50$ 分的暴力都只有二十来行代码,然而包括我在内的很多人在考场上都没有写出来,连 $O(n^2)$ 的暴力都没想到,最后写了个 $O(n^3)$ 的 dp 还假了。/kk
T3,不算难的大模拟,但是很搞人心态,特别是对于理解错题目或者调不出来的,基本上要几乎一次性写对才算是有利。
T4,树上航空管制,思维上甚至没有 T2 难。代码实现上有很多细节和优化,两个 $\log$ 的时间复杂度可能还需要一点点卡常。
另一方面,本次 CSP-S 题目质量偏低,推测是为了给 NOIP 留题。尤其是图论和数据结构,值得注意。
洛谷为这四题评的是橙蓝绿蓝,没什么问题。
附录
原题链接
参考文献
很多游记,这里就不放链接了
版权信息
本文原载于reincarnatey.net,遵循CC BY-NC-SA 4.0协议,复制请保留原文出处。